Beregning af en baldakin lavet af polycarbonat og et profilrør: procesfunktioner

Emnet for denne artikel er beregningen af en polycarbonat baldakin med egne hænder. Vi skal lære at beregne hovedparametrene for strukturen forbundet med dens styrke og dimensioner. Så lad os gå.

Det er denne type baldakiner, vi skal diskutere.

Indhold

Hvad beregner vi

Vi skal lære at beregne:

Tykkelsen af polycarbonatet og kassens stigning afhængig af forventet snebelastning pr. kvadratmeter.
Bueafdækningsmål (hvilket i form af geometri går ud på at beregne længden af buen).

For at præcisere: vi udforsker måder at beregne buen for kendt radius og vinkel for sektoren, såvel som for det tilfælde, hvor vi kun kender afstandene mellem de yderste punkter på bueoverfladen.

Minimum rørsektion med kendt bøjningsbelastning.

I denne rækkefølge går vi videre.

Drejning og belægningstykkelse

Lad os starte med beregningen af snebelastningen.

Inden vi finder ud af, hvordan man beregner en polycarbonat baldakin, vil vi formulere et par antagelser, som beregningen er baseret på.

De givne data er relevante for materiale af høj kvalitet uden tegn på ødelæggelse af ultraviolet stråling. Polycarbonat uden UV-filter bliver skørt efter 2-3 års drift i lyset.

Fraværet af et ultraviolet filter forårsager accelereret nedbrydning af polycarbonat.

Vi ignorerer bevidst kassens begrænsede deformationsstabilitet, idet vi betragter den som absolut stærk.

Og nu - et bord, der hjælper dig med at vælge den optimale tykkelse af polycarbonat og kassens stigning.

Belastning, kg/m2	Kassecelledimensioner med polycarbonattykkelse, mm
Belastning, kg/m2	6	8	10	16
100	1050x790	1200x900	1320 x 920	1250x950
	900x900	950x950	1000x1000	1100x1100
	820 x 1030	900x1100	900x1150	950x1200
160	880x660	1000x750	1050x750	1150x900
	760 x 760	830x830	830x830	970 x 970
	700x860	750x900	750 x 950	850 x 1050
200	800x600	850x650	950x700	1100x850
	690 x 690	760 x 760	780 x 780	880x880
	620 x 780	650x850	700x850	750 x 950

Arch

Beregning efter radius og sektor

Hvordan beregner man buen for en baldakin, hvis vi kender bøjningsradius og buesektor?

Læs også: Hustagsordning: grundlæggende muligheder

Formlen vil se ud som P=pi*r*n/180, hvor:

P er længden af buen (i vores tilfælde længden af et polycarbonatark eller et profilrør, som bliver et element i rammen).
pi er tallet "pi" (i beregninger, der ikke kræver ekstrem høj nøjagtighed, normalt taget lig med 3,14).
r er buens radius.
n er buevinklen i grader.

Lad os som et eksempel med vores egne hænder beregne længden af baldakinbuen med en radius på 2 meter og en sektor på 35 grader.

P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 meter.

I arbejdsprocessen opstår ofte den modsatte situation: det er nødvendigt at justere buens radius og sektor til en fast længde af buen. Årsagerne er klare: prisen på polycarbonat er høj nok til at minimere mængden af affald.

I dette tilfælde vil produktet af sektoren og radius naturligvis være lig med P/pi*180.

Lad os prøve at passe buen under et standardark 6 meter langt. 6/3,14*180=343,9 (med afrunding). Yderligere - et simpelt udvalg af værdier med en lommeregner i hånden: for eksempel for en buesektor på 180 grader kan du tage radius lig med 343,9 / 180 \u003d 1,91 meter; med en radius på 2 meter vil sektoren være lig med 343,9 / 2 \u003d 171,95 grader.

Beregning efter akkorder

Hvordan ser beregningen af designet af en polycarbonat baldakin med en bue ud, hvis vi kun har oplysninger om afstanden mellem buens kanter og dens højde?

I dette tilfælde anvendes den såkaldte Huygens-formel. For at bruge det, lad os mentalt dele akkorden, der forbinder enderne af buen, i halve, hvorefter vi tegner en vinkelret på akkorden i midten.

Punkt C er placeret nøjagtigt i midten af segment AB. Punkt M er placeret i skæringspunktet mellem vinkelret på segmentet AB, tegnet fra punkt C, med buens linje.

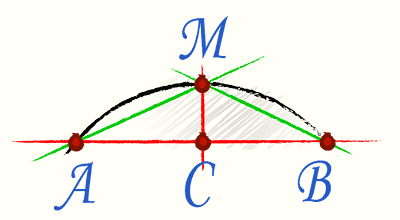
Selve formlen har formen Р=2l+1/3*(2l-L), hvor l er AM-akkorden og L er AB-akkorden.

Vigtigt: beregningen giver et omtrentligt resultat. Den maksimale fejl er 0,5 %; jo mindre buens vinkelsektor er, jo mindre er fejlen.

Lad os beregne længden af buen for sagen, når AB \u003d 2 m og AM - 1,2 m.

Læs også: Taghældningsberegning: hvilke faktorer skal man overveje

P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 meter.

Beregning af strækningen med kendt bøjningsbelastning

Noget af en livssituation: En del af baldakinen er et visir af kendt længde. Vi kan groft estimere den maksimale snebelastning på den. Hvordan vælger man et profilrør af en sådan sektion til bjælker, så det ikke bøjer under belastning?

På billedet - konsekvenserne af en forkert beregning.

Bemærk! Vi berører bevidst ikke, hvordan man beregner belastningen på baldakinen. Vurdering af sne- og vindbelastning er et helt selvforsynende emne for en separat artikel.

For at beregne har vi brug for to formler:

M = FL, hvor M er bøjningsmomentet, F er kraften påført enden af håndtaget i kilogram (i vores tilfælde vægten af sneen på visiret), og L er længden af håndtaget (længden af bjælken, der bærer belastningen fra sneen, fra kant til punktbefæstelser) i centimeter.
M/W=R, hvor W er modstandsmomentet og R er materialets styrke.

Og hvordan vil denne bunke af ukendte værdier hjælpe os?

I sig selv intet. Nogle referencedata mangler til beregningen.

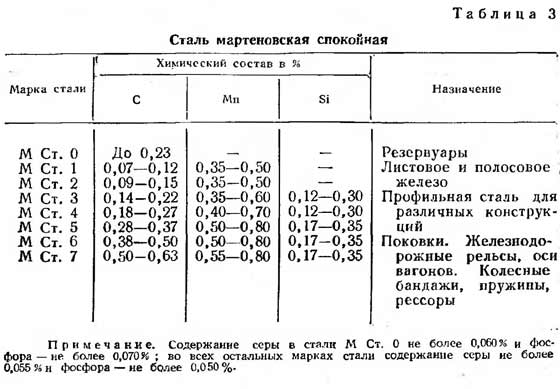
stålkvalitet	Styrke (R), kgf/cm2
St3	2100
St4	2100
St5	2300
14G2	2900
15GS	2900
10G2S	2900
10G2SD	2900
15HSND	2900
10HSND	3400

Reference: St3, St4 og St5 stål bruges normalt til professionelle rør.

Sammensætning og omfang af nogle stålkvaliteter.

Nu kan vi ud fra de data, vi har, beregne profilrørets bøjningsmodstandsmoment. Lad os gøre det.

Antag, at der samler sig 400 kilo sne på en to-meters baldakin med tre bærende bjælker lavet af St3 stål.For at forenkle beregningerne vil vi aftale, at hele belastningen falder på kanten af visiret. Naturligvis vil belastningen på hver bjælke være 400/3=133,3 kg; med en to-meters håndtag vil bøjningsmomentet være lig med 133,3 * 200 \u003d 26660 kgf * cm.

Nu beregner vi modstandsmomentet W. Ud fra ligningen 26660 kgf * cm / W = 2100 kgf / cm2 (stålstyrke) følger det, at modstandsmomentet skal være mindst 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.

Læs også: Skure lavet af træ: billige og nemme at installere strukturer på dit websted

Hvordan vil værdien af modstandsmomentet føre os til rørets dimensioner? Gennem sortimentstabellerne indeholdt i GOST 8639-82 og GOST 8645-68 regulerer dimensionerne af firkantede og formede rør. For hver størrelse angiver de det tilsvarende modstandsmoment og for et rektangulært snit - langs hver af akserne.

Efter at have tjekket tabellerne finder vi ud af, at minimumsstørrelsen på et firkantet rør med de krævede egenskaber er 50x50x7,0 mm; rektangulær (med lodret orientering af den større side) - 70x30x5,0 mm.

En alternativ løsning er at svejse spær fra et mindre rør.

Konklusion

Vi håber, at vi ikke har overanstrengt læseren med en overflod af tørre tal og formler. Som altid kan yderligere oplysninger om metoderne til beregning og design af polycarbonat baldakiner findes i videoen i denne artikel. Held og lykke!

Har artiklen hjulpet dig?